Arbres

Définitions

Un arbre est une structure de donnée A contenant des éléments, tous distincts, appelés sommets et muni des fonctions suivantes:

• la fonction fils(A,p) qui prend en paramètre un arbre A et un sommet p de l’arbre A, et qui renvoie une liste de sommets de A. Ces sommets sont appelés les fils de p.
• la fonction pere(A,f) qui prend en paramètre un arbre A, un sommet f de A et renvoie un sommet de A ou “None”. Le sommet envoyé est appélé le père de f.
• la fonction racine(A) qui prends en paramètre un arbre A et renvoie un sommet de A appelé racine de A.

Pour que (A,racine,fils,pere) soit un arbre, il faut que les propriétés suivantes soient vérifiées :

• la fonction racine(A) prends en paramètre un arbre A et renvoie un sommet de A appelé racine ou None si A est vide.
• Par convention on étend pere de sorte que pere(A,None) = None.
  1. Une racine n’a pas de père : père(A,racine(*)) = None.
  2. Tout sommet a un père à l’exception de la racine : ∀s ∈A/{racine(A)} pere(A,s)∈A → Traduction : pour tout sommet s de A privé des éléments de l’ensemble qui ne contient que la racine A.

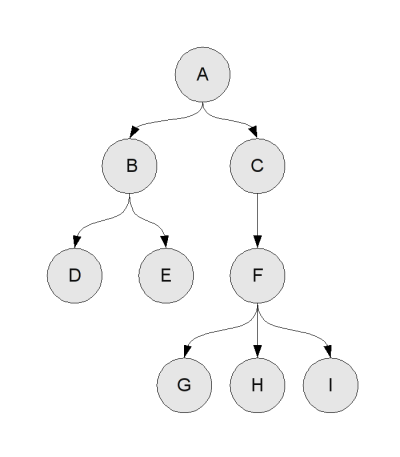Ref : Openclassroom : Algo

1. Les fils d’un sommet s ont pour père s, et le pere p d’un sommet s admet s comme fils.
   • ∀s ∈A, ∀f ∈fils(A,s) pere(A,f) = s → Traduction : pour tout sommet de A, pour tout sommet appartenant aux fils de s, le pere de f est s.
   • ∀s ∈μ, ∀p ∈pere(A,μ) μ∈fils(A,p)
2. Il y a un unique sommet s tels que pere(s) = None et le sommet est la racine.
3. A partir de tout sommet, on peut accéder à la racine par la relation de paternité. ∀s ∈A, ∋k∈N pere^k(A,s) = None. Où pere^k se définit récursivement par :
   • pere⁰(A,s) = s
   • pere^k(A,s) = pere(pere^k-1(A,s))

Exemple :

Est-ce que le quadruplet(A,racine,pere,fils) est un arbre ? Si oui dessinez le :

• A = {1,2,8,9,5,7}
• pere :
  • 9:1
  • 2:9
  • 5:9
  • 7:None
  • 1:2
  • 8:9
• racine(A) = 7
• fils :
  • 1:{9}
  • 2:{1}
  • 9:{2,5}
  • 5:{}
  • 8:{}
  • 7:{}

Non ce n’est pas un arbre car la règle 5 n’est pas vérifiée : pere(pere(pere(2))) = 2. De plus la règle 3 n’est pas vérifiée non plus : pere(8)=9 et 8∉fils(9).

Exercice : Est-ce que le quadruplet(A,racine,pere,fils) est un arbre ? Si oui dessinez le :

• A = {a,1,’toto’,9}
• pere :
  • a:1
  • 9:1
  • 1:’toto’
  • ‘toto’=None
• racine(A) = ‘toto’
• fils :
  • a:{}
  • 1:{a,9}
  • ‘toto’:{1}
  • 9:{}

Attention : Pour l’instant nos arbres n’ont pas d’étiquettes !!

Exercice : Retranscrire un arbre en quadruplet :

• A{0,1,2,3,5,4}
• pere :
  • 0:None
  • 1:0
  • 2:0
  • 3:2
  • 5:2
  • 4:2
• fils :
  • 0:{1,2}
  • 1:{}
  • 2:{3,5,4}
  • 3:{}
  • 4:{}
  • 5:{}

Note : un arbre vide renvoie None.

A = {} racine(A) = None pere(A,s) = {} fils(A,p) = {}

Arbre dans un arbre :

• A = {a→(A={0,1,2};racine = 0 ; pere{0:None;1:0;2:0};fils : {0:{1,2};1:{};2:{}})}) ; b→(A = ∅; racine = None, pere:{}; fils:{})}

Implémentation d’un arbre :

def creer_arbre_vide():
    A=[]
    pere = {}
    fils = {}
    racine = None
    return [A,pere,fils,racine]

def ajouter_racine(T,s):
    #ajoute dans A un sommet
    #s et le définis comme une 
    #racine
    sommet = T[0]
    pere = T[1]
    fils = T[2]
    assert (p in sommet and not f in sommet)
    T[3] = r
    sommet.append(r)
    pere[r] = None
    fils[r] = []

def ajouter_fils(T,f,p):
    #ajoute dans T le sommets
    #et definit p comme son père
    #p existe dans T
    #s n'exsiste pas dans T
    assert (p in sommet and not f in sommet)
    sommet = T[0]
    pere = T[1]
    fils = T[2]
    sommet.append(f)
    pere[f] = p
    fils[f] = []
    fils[p].append(f)

T = creer_arbre()
ajouter_racine(T,1)
ajouter_fils(T,2,1)
ajouter_fils(T,3,1)
ajouter_fils(T,4,1)
ajouter_fils(T,9,3)

def pere(T,s):
    pere = T[1]
    return pere[s]
def fils(T,s):
    fils = T[2]
    return fils[s]
def racine(T):
    racine = T[3]
    return racine

Un arbre étiqueté est un arbre muni d’une opération supplémentaire : def etiquette(T,s) qui prend en paramètre un abre T et un sommet s et qui renvoie un éléement appelé etiquette de s.

Exemple :

• Sommet = {1,2,4}
• racine = 1
• pere :
  • 1:None
  • 2:1
  • 4:1
• fils :
  • 1:{2,4}
  • 2:{}
  • 4:{}
• etiquette = {1:”b”,4:”a”,2:”a”}

Les etiquettes de deux sommets peuvent être identiques.

Attention :

Dans de très nombreux cas l’identifiant des sommets sont unis et remplacés par leurs etiquettes. C’est un abus de notation !!

Définiton :

La taille d’un arbre est son nombre de sommets. Dans un arbre, la hauteur d’un sommet s est le plus petit entier h >= 0 tel que:
pere^h(T,s)= racine(T) \(min(h \in \mathbb{N}) \Rightarrow pere ^h (A,s) = racine(A)\)

La hauteur d’un arbre est la hauteur maximale de ses sommets.

Exemple:

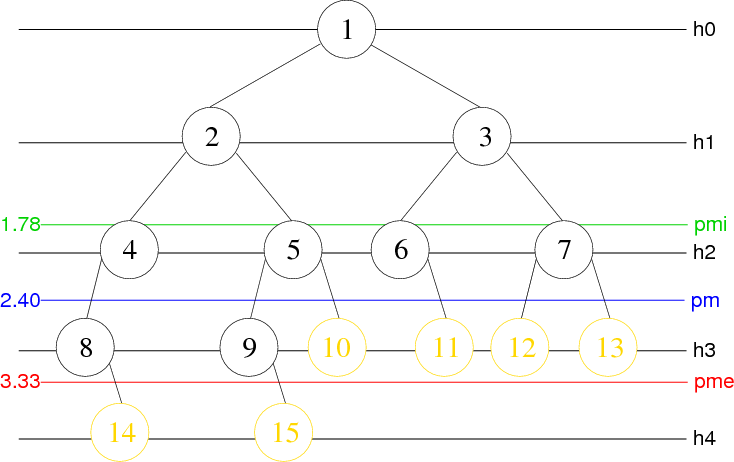
Ref : Site Epita

• $pere ^2 (A,4) = 1 = racine(T)$
  • hauteur(4) = 2
• $pere ^0 (A,1) = 1 = racine(T)$
  • hauteur(1) = 0

On dit qu’un sommet s est un ancêtre de t ou bien que t est un descendant de s si: \(\exists k \in \mathbb{N} \Rightarrow pere ^k (A,t)=s\)

On appelle un sous arbre A’ d’un arbre A au sommet s, l’arbre dont :

• les sommets sont les descendants de s dans A
• les fonctions peres et fils de A’ sont les restrictions de père et fils de A aux descendants de s hormis pour le sommet s où $pere(A’,s) = None$
• la racine est s.

Exemple : 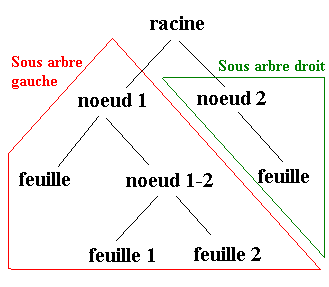Ref : Site daily info

Tous les sommets à hauteur h d’un arbre est appelé le niveau h de l’arbre.

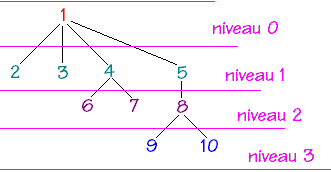
Ref : Developpez.com

On appelle une feuille un sommet qui n’a pas de fils.

On appelle noeud interne un sommet qui a au moins un fils.

On appelle aussi noeud externe une feuille.

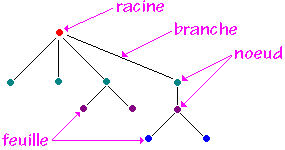
Ref : Developpez.com

Note : Dans ce cours, profondeur et hauteur sont des synonymes.

Arbres binaires

Un arbre binaire est une structure de données A contenant des éléments appelés sommets munis des fonctions suivantes:

• La fonction fils gauche(A,P) prends en paramètre un arbre A, un sommet P et renvoie un sommet de A appelé fils gauche de P ou None si P n’a pas de fils gauche.
• La fonction fils droit(A,P) prends en paramètre un arbre A, un sommet P et renvoie un sommet de A appelé fils droit de P ou None si P n’a pas de fils doit.
• La fonction père(A,F) qui prend en paramètre un arbre A et un sommet F et qui retourne un sommet de A ou None.. Ce sommet est appelé le père de F.
• La fonction racine(A) prends en paramètres un arbre A et renvoie un sommet de A appelé racine de l’arbre.

Ces opérations vérifient les propriétés suivantes:

• Une racine n’as pas de père
  • $pere(A, racine(A)) = None$
• Tout sommet a un père à l’exception de la racine
  • $\forall s \in A / {racine} : pere(A,s) \in A$
• A partir de tout sommet on peut acceder à la racine par la relation de paternité
  • $\forall s \in A : \exists k \in \mathbb{N}\ tq\ pere^k(A,s) = None$
• Le fils gauche d’un sommet s a pour père s:
  • $\forall s \in A , fils_{gauche}(A,s) \neq None \Rightarrow pere(A,fils_gauche(A,s)) = s$
• Le fils droit d’un sommet s a pour père s:
  • $\forall s \in A , fils_{droit}(A,s) \neq None \Rightarrow pere(A,fils_droit(A,s)) = s$

On appelle arbre binaire étiqueté un arbre binaire A muni de l’opération étiquette(A,s) qui à un sommet s renvoie son étiquette

Exemple :

• Sommet = {1,2,3,4,5}
• racine = 1
• pere :
  • 1:None
  • 2:1
  • 3:1
  • 4:3
  • 5:2
• fils_gauche :
  • 1:2
  • 2:None
  • 3:4
  • 4:None
  • 5:None
• fils_droit :
  • 1:3
  • 2:5
  • 3:None
  • 4:None
  • 5:None
• etiquette = {1:”a”,2:”a”,3:”b”,4:”b”,5:”c”}

Parcours d’un arbre binaire

Il existe plusieurs façon de parcourir les sommets d’un arbre. On peut les parcourir par niveau. Mais pour les arbres binaires, il existe 3 parcours supplémentaires : prefixe, infixe et postfixe.

Le parcours prefixe se définit récursivement par :

• $prefixe(A) = prefixe(A,racine(A))$
• $prefixe(A,s) = [s] + prefixe(fils_{gauche}(A,s)) + prefixe(fils_{droit}(A,s))$
• $prefixe(A,None) = []$

Le parcours infixe n’est disponible que pour les arbres binaires, il se définit ainsi:

• $infixe(A) = infixe(A,racine(A))$
• $infixe(A,s) = infixe(A,fils_{gauche}(A,s)) + [s] + infixe(A,fils_{droit}(A,s)))$
• $infixe(A,None) = []$

Le parcours postfixe se définit de la façon suivante :

• $postfixe(A) = postfixe(A,racine(A))$
• $postfixe(A,s) = postfixe(A,fils_{gauche}(A,s)) + postfixe(A,fils_{droit}(A,s))) + [s]$
• $(A,None) = []$

Ces parcours jouent un rôle important dans l’étude des programmes.

Note :

• prefixe utile pour savoir dans quel ordre les programmes se sont exécutés
• postfixe utile pour savoir dans quel ordre les programmes se sont terminés
• infixe pratique pour le trie dans le cas des arbres binaires de recherche

Un arbre binaire de recherche est un arbre binaire étiqueté, dont les étiquettes sont des éléments totalement ordonnés (par exemple des entiers), tels que pour tout sommet s les étiquettes du sous arbre gauche sont toutes plus petites ou égales que l’étiquette de s. Et, les étiquettes du sous arbre droit sont toutes strictement plus grande que l’étiquette de s.

Note : on rappelle qu’un ensemble E est totalement ordonné si toutes paires d’élement est comparable par une relation de comparaison <).

Propriété : le parcours infixe d’un arbre binaire de recherche renvoie la liste des sommets trié par ordre croissant. (marche pour l’ordre lexicographique).

Un arbre binaire de recherche est équilibré si pour tous sommet s de l’arbre :

(hauteur_sous_arbre_gauche(s)) - (hauteur_sous_arbre_droit(s)) ≤ 1